# Vector3
- 描述
用于表示 3D 向量和点。
可以使用该结构保存与计算 3D 位置和方向。 此外,它还包含用于执行常见向量操作的函数。
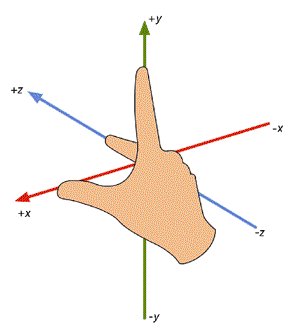
MC中使用的是右手坐标系,如下图所示。后文中的上下前后左右均是以steve面向z轴正方向得出来的。MC中东西方向为X坐标轴,其中X轴正方向为东,X轴负方向为西;南北方向为Z坐标轴,其中Z轴正方向为南,Z轴负方向为北。即左西右东前南后北。
# 构造函数
# Vector3(x, y, z)
描述
用于构造一个向量或者3维点坐标。
参数
参数名 数据类型 说明 x float 向量的x分量 y float 向量的y分量 z float 向量的z分量 返回值
数据类型 说明 Vector3 返回Vector3(x, y, z) 示例
from common.utils.mcmath import Vector3
newOne = Vector3(1, 2, 3)
# Vector3(vecTuple)
描述
用于构造一个向量或者3维点坐标。
参数
参数名 数据类型 说明 vecTuple tuple(float, float, float) 长度为3的tuple数组 返回值
数据类型 说明 Vector3 返回Vector3(vecTuple[0], vecTuple[1], vecTuple[2]) 示例
from common.utils.mcmath import Vector3
import client.extraClientApi as clientApi
comp = clientApi.CreateComponent(entityId, "Minecraft", "pos")
entityFootPos = comp.GetFootPos() # 通过位置组件获取实体位置
posVec = Vector3(entityFootPos) # 直接将该位置tuple转换成Vector3以便后续计算
# 静态方法
可以直接通过Vector3.MethodName()调用的静态方法,无需创建实例。
# One
描述
用于编写 Vector3(1, 1, 1) 的简便方法。
返回值
数据类型 说明 Vector3 返回Vector3(1, 1, 1) 示例
from common.utils.mcmath import Vector3
newOne = Vector3.One()
# Up
描述
用于编写 Vector3(0, 1, 0) 的简便方法。
返回值
数据类型 说明 Vector3 返回Vector3(0, 1, 0) 示例
from common.utils.mcmath import Vector3
newOne = Vector3.Up()
# Down
描述
用于编写 Vector3(0, -1, 0) 的简便方法。
返回值
数据类型 说明 Vector3 返回Vector3(0, -1, 0) 示例
from common.utils.mcmath import Vector3
newOne = Vector3.Down()
# Left
描述
用于编写 Vector3(-1, 0, 0) 的简便方法,对应MC中的西面。
返回值
数据类型 说明 Vector3 返回Vector3(-1, 0, 0) 示例
from common.utils.mcmath import Vector3
newOne = Vector3.Left()
# Right
描述
用于编写 Vector3(1, 0, 0) 的简便方法,对应MC中的东面。
返回值
数据类型 说明 Vector3 返回Vector3(1, 0, 0) 示例
from common.utils.mcmath import Vector3
newOne = Vector3.Right()
# Forward
描述
用于编写 Vector3(0, 0, 1) 的简便方法,对应MC中的南面。
返回值
数据类型 说明 Vector3 返回Vector3(0, 0, 1) 示例
from common.utils.mcmath import Vector3
newOne = Vector3.Forward()
# Backward
描述
用于编写 Vector3(0, 0, -1) 的简便方法,对应MC中的北面。
返回值
数据类型 说明 Vector3 返回Vector3(0, 0, -1) 示例
from common.utils.mcmath import Vector3
newOne = Vector3.Backward()
# Dot
描述
两个向量的点积。
点积是一个浮点值,它等于 将两个向量的大小相乘,然后乘以向量之间角度的余弦值。
对于 normalized 向量,如果它们指向完全相同的方向,Dot 返回 1; 如果它们指向完全相反的方向,返回 -1;如果向量彼此垂直,则 Dot 返回 0。
参数
参数名 数据类型 说明 a Vector3 向量a b Vector3 向量b 返回值
数据类型 说明 float 两个向量的点积 示例
from common.utils.mcmath import Vector3
a = Vector3(1, 2, 3)
b = Vector3(0, 3, 1)
c = Vector3.Dot(a, b) # 1 * 0 + 2 * 3 + 3 * 1 = 9
# Cross
描述
两个向量的叉积。
两个向量的叉积生成第三个向量, 该向量垂直于两个输入向量。结果的大小等于: 将两个输入的大小相乘,然后乘以输入之间角度的正弦值。 可以使用“右手定则”确定结果向量的方向。用右手的四指先表示向量a的方向,然后手指朝着手心的方向摆动到向量b的方向,大拇指所指的方向就是向量c的方向。
参数
参数名 数据类型 说明 a Vector3 向量a b Vector3 向量b 返回值
数据类型 说明 Vector3 两个向量的叉积 示例
from common.utils.mcmath import Vector3
a = Vector3(1, 2, 3)
b = Vector3(0, 3, 1)
c = Vector3.Cross(a, b)
# 成员方法
# x
描述
返回该向量的x坐标值。
返回值
数据类型 说明 float 该向量x的坐标值 示例
from common.utils.mcmath import Vector3
a = Vector3(3.0, 4.0, 0.0)
print a.x # 打印 3.0
# y
描述
返回该向量的y坐标值。
返回值
数据类型 说明 float 该向量y的坐标值 示例
from common.utils.mcmath import Vector3
a = Vector3(3.0, 4.0, 0.0)
print a.y # 打印 4.0
# z
描述
返回该向量的z坐标值。
返回值
数据类型 说明 float 该向量z的坐标值 示例
from common.utils.mcmath import Vector3
a = Vector3(3.0, 4.0, 0.0)
print a.z # 打印 0.0
# Length
描述
返回该向量的长度。
向量长度为
(x*x+y*y+z*z)的平方根。如果只需要比较一些向量的大小, 则可以使用LengthSquared()函数比较它们的平方数(计算平方数更快)。
返回值
数据类型 说明 float 该向量的长度 示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
print a.Length() # 打印 5.0
# LengthSquared
描述
返回该向量的长度的平方。
返回值
数据类型 说明 float 该向量的长度的平方 示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
print a.LengthSquared() # 打印 25.0
# ToTuple
描述
返回该向量的tuple形式(x, y, z),便于玩家转换后作为其他事件的参数进行传递。
返回值
数据类型 说明 tuple 返回该向量的tuple形式(x, y, z) 示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
print a.ToTuple() # 打印 (3, 4, 0)
# Normalized
描述
返回长度为 1 时的该向量。
进行标准化时,向量方向保持不变,但其长度为 1.0。
请注意,当前向量保持不变,返回一个新的归一化向量。如果 要归一化当前向量,请使用Normalize函数。
如果向量太小而无法标准化,则返回零向量。
返回值
数据类型 说明 Vector3 该向量标准化后的向量 示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
print a.Normalized() # 打印结果(0.6, 0.8, 0)
print a # 打印结果(3, 4, 0),a并没有发生变化
# Normalize
描述
使该向量标准化,向量方向保持不变,但其长度变为 1.0。
请注意,该函数无返回值,仅改变当前向量,如果要返回当前向量的标准化值且不改变该向量,请使用Normalized函数。
如果向量太小而无法标准化,则设置为零向量。
示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
a.Normalize()
print a # 打印结果(0.6, 0.8, 0),a被标准化
# Set
描述
设置该向量的值
参数
参数名 数据类型 说明 x float 向量的x分量 y float 向量的y分量 z float 向量的z分量 示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
a.Set(1, 2, 3)
print a # 打印结果(1, 2, 3)
# 成员变量
描述
可以直接通过
.运算符访问向量的x、y、z分量。也可以通过[]直接获取,0、1、2分别对应x、y、z。但不能直接通过该方法对各个分量进行设置,只能通过Set方法来进行设置。示例
from common.utils.mcmath import Vector3 a = Vector3(3, 4, 5) print a.x # 3 print a.y # 4 print a.z # 5 print a[0] # 3 print a[1] # 4 print a[2] # 5
# 运算符
# operate +
描述
向量加法,两向量相加等于各分量之和。向量与常数相加等于各分量分别加上该常数。
示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
b = Vector3.One()
print a + 5 # 打印结果(8, 9, 5)
print a + b # 打印结果(4, 5, 1)
# operate -
描述
向量减法,两向量相加等于各分量之差。向量与常数相减等于各分量分别与该常数求差。
向量求反,返回相反方向的向量
示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
b = Vector3.One()
print a - 2 # 打印结果(1, 2, -2)
print 2 - a # 打印结果(-1, -2, 2)
print a - b # 打印结果(2, 3, -1)
print -a # 打印结果(-3, -4, 0)
# operate *
描述
向量乘法,两向量相乘等于各分量相乘相加,即向量点积,等价于Vector3.Dot(a, b)。向量与常数相乘等于各分量分别乘以该常数。
示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
b = Vector3.Up()
print a * 2 # 打印结果(6, 8, 0)
print a * b # 打印结果4
# operate /
描述
向量除法,仅支持向量与常数相除,等于各分量分别除以该常数。
示例
from common.utils.mcmath import Vector3
a = Vector3(3, 4, 0)
b = Vector3.One()
print a / 2 # 打印结果(1.5, 2, 0)
# operate ==
描述
判断两个向量是否相等,当各分量均相等时返回True
# operate !=
描述
判断两个向量是否不等,当各分量均相等时返回False
入门
分钟
← 我的世界基础概念 Quaternion →



